前言
匆匆忙忙搬家后,近十日没有更新博客了,因为实验室工作还没有开始所以最近还算比较清闲。有时间的话基本在看机器学习相关。越学越觉得自己数学基础好差哈哈哈。
因为 CS224n 和 CS229 是同时在看(其实后者应该是前者的前置课程),所以就同时把进度更新在博客了。
Lecture 1 看的非常早,大三下学期上课的过程中就刷完了,Lecture 2 被拖延症拖到现在没看完。于是!神奇的博主啊,他选择看 Lecture 3!(病入膏肓
所以之后回头刷完 Lecture 2 会补在前面吧lol
参考资源:
- https://www.bilibili.com/video/BV1Eb411H7Pq?p=3 CS224n Lecture 3
- https://blog.csdn.net/weixin_34378969/article/details/88021990 Softmax
正文
背景知识
致像我一样急功近利没刷完机器学习就来看NLP的同学。
Softmax
Lecture 3 - 09:08 提到了 softmax 分类器。Manning 提到 softmax 与 Logistic 分类非常接近。下面是 Softmax 分类的公式。
$$ P(i)=\dfrac{exp(\theta_i^Tx)}{\sum_{k=1}^{K}exp(\theta_k^Tx)} $$
找了一些资料感觉其实 Softmax 并没有很难,基本思路在于:手上现在有几个不同的数据,我现在需要给每个数据分配一个概率,数据越大要有越大的概率,但是较小的数据也要有概率,且所有数据的概率和应该为 1 。那么使用上面的公式就可以完成。分子是指数函数,当 $\theta_i^Tx$ 越大,概率就会越大,而分母是所有类别的 $\theta_i^Tx$ 的求和,这就使得最终所有的概率相加和为 1 。
Cross-Entrophy
参考 https://zhuanlan.zhihu.com/p/35709485
High-bias
与 High Variance 相对应。在吴恩达的视频课程中以及西瓜书中都有提到。也被叫做欠拟合,High-bias是在说模型学习的训练数据太少,所以判断依据主要是少量的训练数据,故而没能学到 universal 的特征与输出的关系。
主要原因(可能记得不大清了,之后过CS229再回头改吧):模型参数过多(比如一个深度神经网络),训练数据过少。
representational learning
https://zhuanlan.zhihu.com/p/112849395
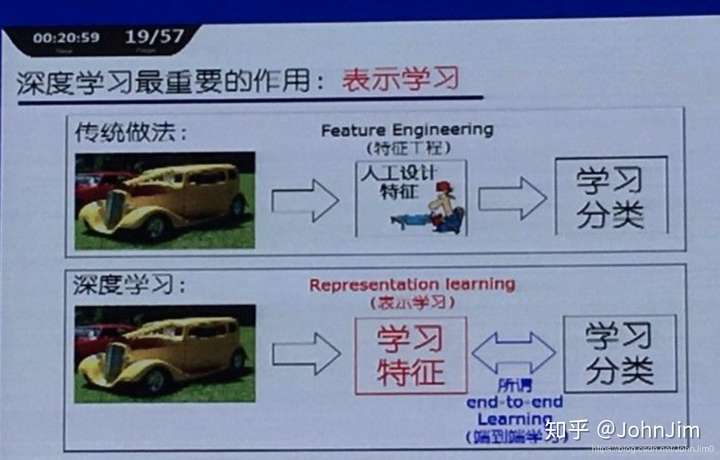
大意是去学习数据的特征,将数据以更好的形式表达,以达到更好的学习效果。比如一个图像,先学习出一个向量表示其各个部分的特征,接下来使用这个向量代替图片来进行分类学习,以提升效果。(这么一来词向量的学习也许也算这个?
Jacobian Matrix
对于一个多输入多输出的函数求梯度,其梯度就是一个 Jacobian Matrix。
参考 http://web.stanford.edu/class/cs224n/slides/cs224n-2020-lecture04-neuralnets.pdf

下面给出 slides 中提到的一些 Jacobian matrices。
https://www.jianshu.com/p/8aa646fad1c5 Latex 导数相关语法
1 | $ \frac{\partial f}{\partial x} $ |
$$ \frac{\partial}{\partial x}(Wx+b)=W $$
$$ \frac{\partial}{\partial b}(Wx+b)=I $$ ($I$ 是单位矩阵)
$$ \frac{\partial}{\partial u}(u^Th)=h^T $$
知识点
在 NLP 的深度学习中,通常同时学习参数( $\theta$ ) 以及词向量。
We learn both W and word vectors x.
We learn both conventional parameters and representations.
对于 NER ( Named Entity Recognition) ,因为要考虑 Context :
- 最简单的思路:画一个 Window 圈住 Context , 求里面每个单词的词向量的平均,然后扔进分类器学习。It loses the position information!
- 将几个单词的词向量按顺序连成一个大的向量。比如我们的 window 包括前后两个单词,那么我们分类器的输入就是 $5D$ 维度的向量,其中 $D$ 是一个词向量的维度。