前言
最近真的是疯狂挖坑啊…… 看到什么都想学,只要和专业课无关或者只是他们的扩展就学的十分上头哈哈哈,人类神奇的心理。经过这学期比较硬核的专业课的学习(尤其是软件安全),也在反思自己是否在学习自己喜欢的东西,是否还有刚上大学,刚学编程语言时的那种兴奋感与快乐。之前受到各个方面的影响,总觉的学了安全以后的就可以当大黑阔,如看门狗中的能力,低头看一眼手机,周围的设备仅在掌控,实际上哪里有那么容易,挖到一个 0 day 漏洞背后不知道是多少基本功上的努力,看了多少汇编(令人头秃),而这类人才是非常非常稀有的,就像再次高考筛选一波 985 和清北的感觉一样。
最近学信息内容安全,之前第一反应是这个课大概就是监督舆论之类,抱着蹭 GPA 的心态来,不过学了以后发现是这个学期最为惊喜的一门课了。涉及到了机器学习、NLP、还有爬虫等很多之前就想试试看的领域。而在课程中,老师强推了 CS224n,大概看了以后感觉自己好菜啊……所以最近也在准备的了解一波基础知识。除去这些,其实个人对语言还是蛮感兴趣的,所以对NLP也有一点好奇,于是又找到了尘封多年的 吴恩达老师的机器学习 公开课开始学习。
课件相关资料:
- https://www.coursera.org/learn/machine-learning/resources/QQx8l 需要注册 Coursera 上的 ML 课程
正文
之前试水的时候其实已经将第一章节看完了,基本上都是一些基本概念,所以这次也不打算重头再看,直接从单变量线性回归开始。
前几节看的感觉非常不错,基本上一点五倍速还是能稳稳跟上的,老师讲的是非常的细致直接易懂,感觉学的很舒服。下面贴一些看的过程中自己觉得比较有意思的知识点。

上面的图是在讲梯度下降时的图片,重点在下面的两种方法的对比,左侧是所谓的同步,而右边则并没有同步(求完偏导之后就更新了theta,然后这时候在对另一个theta进行求偏导)。老师介绍道,左侧的方法更为自然,同时经过实践显示效果更好。
插播线性代数
对于没有逆矩阵的矩阵,我们叫它 奇异矩阵(singular) 或者 退化矩阵(degenerate)
Feature Scaling
对于多变量的线性回归,使用梯度下降算法,如果变量之间的量级不再一个级别,会使得 损失函数 $J(\theta)$ 的等高图显示的像一个细长、尖的椭圆,这时梯度下降会走很多不必要的路线,会左右摇荡。如果我们对于每个变量根据取值范围做一定的缩放,使他们的量级在一个数量级,就可以让等高图变得更远,这样子梯度下降过程会更快。
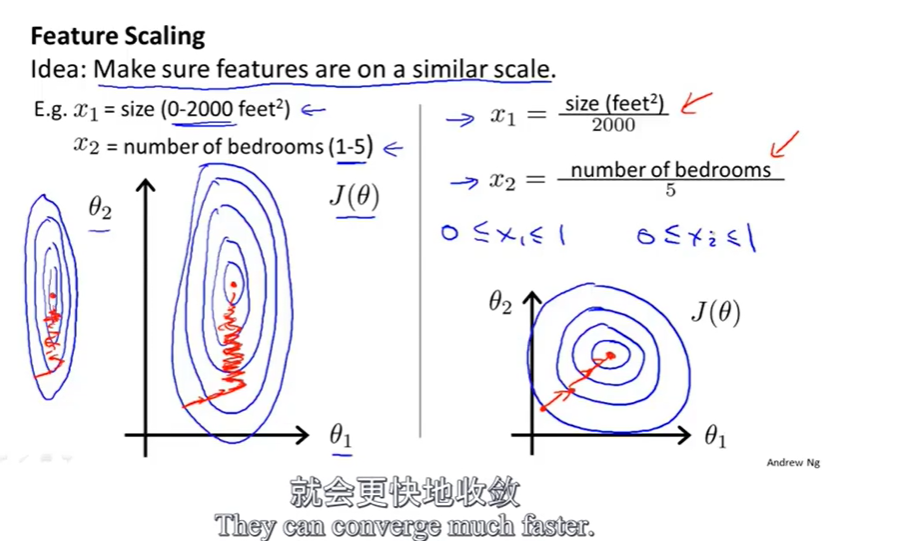
关于缩放的量级,一般会缩放使得变量范围在正负一之间,吴恩达教授个人建议如果范围在 正负 3 之间,或者 正负三分之一之间都是OK的。
正规方程 Normal Equation
除了使用梯度下降的迭代方法,还有一种一步到位的方法。
设参数 $\theta$ 是一个 n + 1 维的向量,X 是 一个 $m * (n + 1)$ 的矩阵,其中 m 是样本数量, $x_0 = 1$ 。y 是一个 m 维向量,每个维度值代表对应样本的函数值。
解 theta 的方程如下。
$$
\theta = (X^TX)^{-1}X^Ty
$$
对应的 Octave 代码如下:
1 | pinv(X' * X) * X' * y |
值得一提的是,正规方程法不需要做 feature scaling。
下面是正规方程法与梯度下降法的对比,结论是 在 n 小于等于 10000 时考虑使用正规方程法(吴恩达老师拍摄视频时的推荐,也许随着计算机速度的提升,近些年我们可以对更大的 n 使用正规方程法), n 过大时采用梯度下降法。因为 矩阵乘法的时间复杂度 是 $O(n^3)$ ,当然我们学过算法知道是可以优化的。但是也只是优化到 二点几次幂,时间复杂度还是很高的,而我们使用正规方程法要求 X 与 其转置的乘积,所以当 n 过大时会造成速度过于缓慢。
| Gradient Descent | Normal Equation |
|---|---|
| 需要选择 alpha 学习率 | 不需要选择学习率 |
| 需要多次迭代 | 不需要迭代 |
| 当 n 很大时依然能正常运作 | 当 n 变得过大以后运算十分缓慢 |
当 $X^TX$ 不可逆的时候,使用 Octave 的 pinv 依然可以得到我们需要的 theta ,但是吴恩达教师没有给我们做深入解释。此外这种情况不太常见,如果发生了,最多的情况是如下2个。
- 有冗余参数,比如 一个参数是单位为平方米的面积,一个参数是单位为平方英尺的面积,这两个是线性关系。
- 参数太多了,尤其是 m <= n 。当样本相比参数来说过少了也会发生这种情况。可以选择删除参数或者使用 regularization 。
Logistic Regression
Logistic Regression 虽然名字里带着 回归 但是其实是一种分类算法。
Logistic Function 和 Sigmoid Function 是一个东西。可以互换。
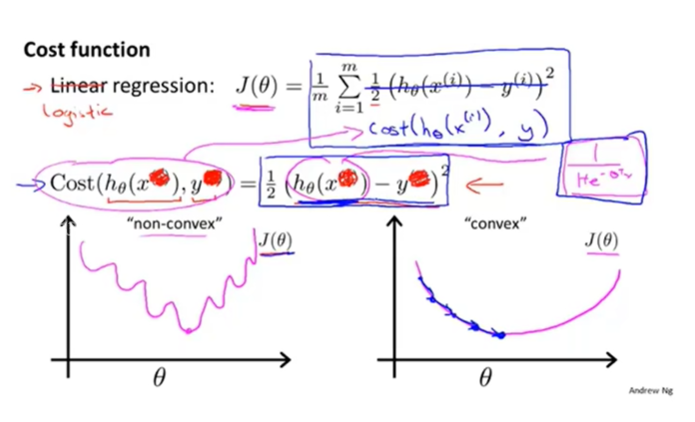
在 Logistic Regression 中,我们不再使用线性回归中的损失函数,因为事实证明,平方的损失函数应用在这里会表现为一个 非凸函数 ,如上图中左边的图像,有非常多的“坑”,如果使用梯度下降算法,很有可能掉进坑里出不去,没有办法拿到全局最优。而我们的目标是一个凸函数,这样使用梯度下降算法就能找到全局最优。
在 Logistic Regression 中使用的损失函数如下。
$$
Cost(h_\theta(x^{(i)},y^{(i)}))=
\left
{
\begin{array}{ll}
-\log(h_\theta(x))&\text{if $y = 1$},\
-\log(1-h_\theta(x))&\text{if $y = 0$}.
\end{array}\right.
$$
这个损失函数是由统计学中的极大似然法得来的。是一种为模型快速寻找参数的方法,另外还是个凸函数。